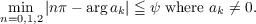|
|||||

|

|
|

|

|
|
Convolution transforms
whose inversion function has complex roots in a wide
angle
Zeev Ditzian |
|
Vol. 27 (1968), No. 3, 485–496
|
Mathematical Subject Classification
Primary: 44.25
|
Milestones
Received: 27 November 1967
Published: 1 December 1968
|
Authors |
| Zeev Ditzian | |
 |
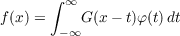
![∫
1-- i∞ −1 st
G (t) = 2πi −i∞[E(s)] ⋅e ds](a071x.png)