|
|||||

|

|
|

|

|
|
Qualitative behavior of
solutions of a third order nonlinear differential
equation
John Willard Heidel |
|
Vol. 27 (1968), No. 3, 507–526
|
Abstract |
|
This paper investigates the behavior of nonoscillatory solutions and the existence of oscillatory solutions of the differential equation 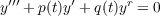 where p(t) and q(t) are continuous and real valued on a half axis [a,∞) and r is the quotient of odd positive integers. The two cases p(t),q(t) ≦ 0 and p(t),q(t) ≧ 0 are discussed. One theorem improves an oscillation criterion of Waltman [16]. Other results supplement those obtained by Lazar [10]. |
Mathematical Subject Classification
Primary: 34.42
|
Milestones
Received: 26 July 1967
Published: 1 December 1968
|
Authors |
| John Willard Heidel | |
 |
