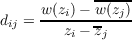|
Let w(z) be a function in
the open upper half plane (UHP) with values in UHP, and let Pn = (dij) be the
n × n matrix of difference quotients
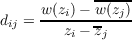
formed from any n points z1,z2,⋯,zn ∈ UHP. It was shown by G. Pick that
if w(z) is also analytic in UHP, then the Pn are all nonnegative definite
Hermitian matrices (denoted Pn ≧ 0). In what follows, two converse results are
derived.
(1) If D is a domain in UHP, w(z) is continuous in D and has values in UHP, and
P3 ≧ 0 for all choices of the z1,z2,z3 ∈ D, then w(z) is analytic in D. It is well
known that the condition P2 ≧ 0 does not imply anything of this sort, but
corresponds only to a distance-shrinking property of w(z) in the noneuclidean
geometry of UHP.
(2) If w is as before, but Pn ≧ 0 for all n and all z1,⋯,zn ∈ D, i.e.,
{w(z) −w(ζ)}∕(z −ζ) is a nonnegative definite kernel in D, then w(z) is
analytic in D and has an analytic extension to UHP whose values are in
UHP.
|