|
|||||

|

|
|

|

|
|
A
new proof of the maximum principle for doubly-harmonic
functions
Henry B. Mann, Josephine Mitchell and Lowell Schoenfeld |
|
Vol. 27 (1968), No. 3, 567–571
|
Abstract |
|
Let f be a real-valued Lebesque integrable function on a domain Ω in Euclidean space E2m, and let f be doubly-harmonic on Ω so that it satisfies 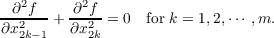 In this paper, a new proof of the maximum principle is given for nonconstant functions f satisfying the preceding conditions. The proof depends on the fact that the associated forms 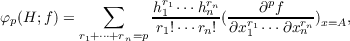 where A ∈ Ω, are either indefinite or identically 0 for each p ≧ 1. The authors previously proved this under weaker hypotheses on f, but the proof used the strong form of the maximum principle for solutions of linear elliptic partial differential equations of the second order with constant coefficients. By means of the theory of distributions, the authors now prove that the φp(H;f) have the stated property without using the maximum principle. Consequently, they obtain a new proof of this principle. |
Mathematical Subject Classification
Primary: 31.30
|
Milestones
Received: 12 September 1967
Published: 1 December 1968
|
Authors |
| Henry B. Mann | |
| Josephine Mitchell | |
| Lowell Schoenfeld | |
 |
