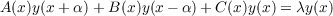Difference equations for some orthogonal polynomials

H. L. Krall and I. M. Sheffer

Vol. 28 (1969), No. 2, 383–392

DOI: 10.2140/pjm.1969.28.383

Abstract

It is well-known that every orthogonal polynomial set {P_n(x)} satisfies a 3-term recurrence relation of the form

(1.1)

Some orthogonal sets (polynomials of Jacobi, Hermite and so on) are solutions of differential equations. It will be shown that there exist orthogonal polynomial sets that satisfy 3-term difference equations of the form

(1.2)

where A, B, C are polynomials of degree ≦ 2 and λ is a parameter.

Mathematical Subject Classification

Primary: 33.40

Secondary: 39.00

Milestones

Received: 12 March 1968

Published: 1 February 1969