A uniqueness theorem for weak solutions of symmetric quasilinear hyperbolic systems

Albert Emerson Hurd

Vol. 28 (1969), No. 3, 555–559

DOI: 10.2140/pjm.1969.28.555

Abstract

The essentially bounded measurable (vector) function u(x,t) = (u₁(x,t),⋯,u_r(x,t)) is called a weak solution of the initial-value problem for the system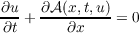

in the upper half-plane t ≧ 0 if it satisfies the usual integral identity (defining “weak”) together with the condition that, given a compact set D in t ≧ 0, there exists a function K(t) ∈ L_loc¹([0,∞)) such that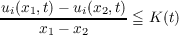

holds a.e. for x₁,x₂ ∈ D and 0 < t < ∞. It is shown that, if the matrix ∂𝒜∕∂u is symmetric and positive definite (a convexity condition), then weak solutions are uniquely determined by their initial conditions.

Mathematical Subject Classification

Primary: 35.57

Milestones

Received: 10 April 1967

Revised: 28 May 1968

Published: 1 March 1969