Some restricted partition functions; Congruences modulo 3

D. B. Lahiri

Vol. 28 (1969), No. 3, 575–581

DOI: 10.2140/pjm.1969.28.575

Abstract

We shall establish in this paper some congruence relations with respect to the modulus 3 for some restricted partition functions. The difference between the unrestricted partition function, p(n), and these restricted partition functions which we shall denote by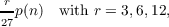

merely lies in the restriction that no number of the forms 27n, or 27n ± r, shall be a part of the partitions which are of relevance in the restricted case. Thus to determine the value of r _ 27p(n) one should count all the unrestricted partitions of n excepting those which contain a number of any of the above forms as a part. We shall assume p(n) and r _ 27p(n) to be unity when n is zero, and vanishing when the argument is negative. We can now state our theorems.

Theorem 1. For almost all values of n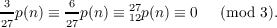

Theorem 2. For all values of n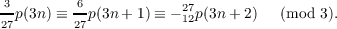

Mathematical Subject Classification

Primary: 10.48

Milestones

Received: 3 October 1967

Revised: 27 May 1968

Published: 1 March 1969