On a conjecture of Golomb

William H. Mills and Neal Zierler

Vol. 28 (1969), No. 3, 635–640

DOI: 10.2140/pjm.1969.28.635

Abstract

On the basis of empirical evidence for n = 2,3,4, and 5 Golomb has conjectured that the degree of every irreducible factor of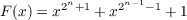

over GF(2) divides 6(n − 1). We prove the stronger result that the degree of every irreducible factor of F(x) divides either 2(n − 1) or 3(n − 1), but not n − 1.

Mathematical Subject Classification

Primary: 12.25

Milestones

Received: 8 June 1968

Published: 1 March 1969