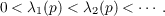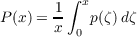Some isoperimetric inequalities for the eigenvalues of vibrating strings

David Clarence Barnes

Vol. 29 (1969), No. 1, 43–61

DOI: 10.2140/pjm.1969.29.43

Abstract

If a string with integrable density function p(x) is fixed at the points x = 0, x = a then the natural frequencies of vibration are determined by the eigenvalues of the Sturm-Liouville System

(1)

These eigenvalues depend on the density function p(x) and we denote them accordingly by λ_n(p),

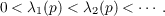
In this work we investigate the nature of the density functions which yield the largest and smallest possible value for λ_n(p) assuming that the average value of the density p(x) defined by

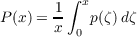
is restricted in some manner.

Mathematical Subject Classification

Primary: 34.30

Secondary: 35.00

Milestones

Received: 22 April 1968

Published: 1 April 1969