Primary Abelian groups modulo finite groups

Ronald J. Ensey

Vol. 29 (1969), No. 1, 77–81

DOI: 10.2140/pjm.1969.29.77

Abstract

Let 𝒜 be the category of Abelian groups, ℱ the Serre class of finite Abelian groups, and form the quotient category 𝒜∕ℱ. The purpose of this paper is to find a complete set of invariants for direct sums of countable reduced p-groups, such groups being considered as objects of the category 𝒜∕ℱ. Specifically, it will be shown that two direct sums of countable reduced p-groups G and H are isomorphic in 𝒜∕ℱ if and only if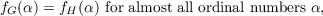

and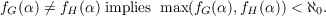

Mathematical Subject Classification

Primary: 20.30

Milestones

Received: 8 January 1968

Published: 1 April 1969