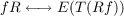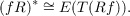|
For each primitive idempotent
f in a left artinian ring R, let T(Rf) denote the unique simple factor of Rf and let
E(T(Rf)) denote its injective hull. Then, identifying a module with its isomorphism
class,
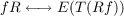
provides a one-to-one correspondence between the finite sets of isomorphism classes
of indecomposable injective left R-modules and indecomposable projective
right R-modules. The importance of this correspondence is illustrated by the
Nagao-Nakayama result that if R is a finite-dimensional algebra over a field K then,
under the duality ( )∗ = HomK(_,K) between the categories of finitely generated
left and right R-modules, one has
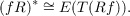
Thus the structure of an indecomposable injective module E(T(Rf)) over such an
algebra R is completely determined by the indecomposable (projective) direct
summand fR of RR. However, in the more general case when R is a left artinian
ring, very little is known about the structure of these indecomposable injective
modules. In this paper we attempt to shed some light on the problem by
showing that a large part of the above mentioned duality can be carried
over to fR and E(T(Rf)) over a ring R with minimum condition on left
ideals.
|