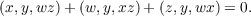|
In 1948 A. A. Albert defined
a standard algebra A by the identities (x,y,z) + (z,x,y) − (x,z,y) = 0
and
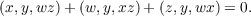
Standard algebras include all associative algebras and commutative Jordan algebras.
The radical R of any finite-dimensional standard algebra A is its maximal nilpotent
ideal. It is known that any semisimple standard algebra is a direct sum of simple
ideals, and that any simple standard algebra is either associative or a commutative
Jordan algebra.
In this paper we study Peirce decompositions and derivations of standard
algebras. We prove the Wedderburn principal theorem for standard algebras of
characteristic ≠2 (announced in 1950 by A. J. Penico for characteristic 0): if A∕R is
separable, then A = S + R where S is a subalgebra of A, S≅A∕R. For standard
algebras of characteristic 0 we prove analogues of the Malcev-Harish-Chandra
theorem and the first Whitehead lemma, and we determine when the derivation
algebra of A is semisimple.
|