|
|||||

|

|
|

|

|
|
On prime divisors of
the binomial coefficient
Earl F. Ecklund Jr. |
|
Vol. 29 (1969), No. 2, 267–270
|
Abstract |
|
A classical theorem discovered independently by J. Sylvester and I. Schur states that in a set of k consecutive integers, each of which is greater than k, there is a number having a prime divisor greater than k. In giving an elementary proof, P. Erdös expressed the theorem in the following form: If n ≧ 2k, then Recently, P. Erdös suggested a problem of a complementary nature: If n ≧ 2k, then The problem is solved by the following Theorem. If n ≧ 2k, then |
Mathematical Subject Classification
Primary: 10.08
|
Milestones
Received: 8 July 1968
Published: 1 May 1969
|
Authors |
| Earl F. Ecklund Jr. | |
 |
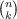 has a prime divisor
has a prime divisor 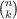 has a prime divisor
has a prime divisor 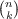 has a prime divisor
has a prime divisor 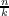
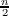
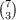 .
.