On finite groups with independent cyclic Sylow subgroups

Marcel Herzog

Vol. 29 (1969), No. 2, 285–293

DOI: 10.2140/pjm.1969.29.285

Abstract

The purpose of this paper is to classify all perfect groups with cyclic Sylow p-subgroups which satisfy the condition

(TI) two different Sylow p-subgroups of G contain only the unit element in common and such that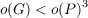

where P is a Sylow p-subgroup of G.

The main result of this paper is the following

Theorem 1. Let G be a perfect finite group with a cyclic Sylow p-subgroup P of order p^a and assume that the Sylow p-subgroups of G satisfy the (TI) condition. Assume, furthermore, that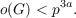

Then one of the following statements holds.

(I) a = 1, G≅PSL(2,p), where p > 3 is a prime.

(II) a = 1, G≅PSL(2,p − 1), where p = 2^m + 1 > 5 is a Fermat prime.

(III) a = 1, G≅SL(2,p), where p > 3 is a prime.

(IV) a = 2, p = 3, G≅PSL(2,8).

Mathematical Subject Classification

Primary: 20.43

Milestones

Received: 10 May 1968

Published: 1 May 1969