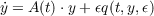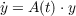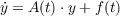|
Consider the nonlinear
differential system
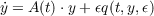 | (1.1) |
where y, q are column n-vectors, q is continuous in (t,y,𝜖) and has continuous second
partial derivatives with respect to y, 𝜖 for all values of t, 0 ≦ y ≦ R for some
R > 0 and 0 ≦ 𝜖 ≦ 𝜖0 for some 𝜖0 > 0. Further assume A(t) is an n × n
matrix such that A ∈ C1, and both A and q are periodic in t with period T.
Associated with system (1.1) are the general homogeneous and nonhomogeneous
equations
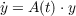 | (1.2) |
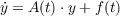 | (1.3) |
where f(t) is an arbitrary n-vector function periodic in t of period T. In this paper
we consider the classical problem of proving the existence of T-periodic solutions
y = y(t) of (1.1) when the homogeneous system (1.2) has nontrivial T-periodic
solutions.
|