Multiplier algebras of biorthogonal systems

Raymond J. McGivney and William Henry Ruckle

Vol. 29 (1969), No. 2, 375–387

DOI: 10.2140/pjm.1969.29.375

Abstract

Let {e_i,E_i} be a total biorthogonal system in a linear topological space X. The multiplier algebra of X with respect to {e_i,E_i} written M(X) is the set of all scalar sequences (t⁽ⁱ⁾) such that for each x ∈ X there is y ∈ X with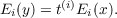

The form of M(X) is determined when {e_i,E_i} is a norming complete biorthogonal system in a Banach space or a basis in a complete barreled space. It is shown that a sequence space is the multiplier algebra for a basis in a Banach space if and only if it is a γ-perfect BK-algebra.

Mathematical Subject Classification 2000

Primary: 46A45

Milestones

Received: 5 August 1968

Published: 1 May 1969