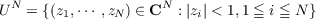|
Let E be a subvariety of the
unit polydisc
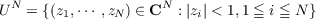
such that E is the zero set of a holomorphic function f on UN, i.e., E = Z(f) where
Z(f) = {z ∈ UN : f(z) = 0}. This amounts to saying that E is a subvariety of pure
dimension N − 1. In [2] Walter Rudin proved that if E is bounded away from the
torus TN = {(z1,⋯,zN) ∈ CN : |zi| = 1,1 ≦ i ≦ N}, then there is a bounded
holomorphic function F on UN such that E = Z(F). Call such a subvariety E, that
is, a pure N − 1 dimensional subvariety of UN bounded from TN, a Rudin variety.
We are interested in the following question: When is it possible to extend every
bounded holomorphic function on a Rudin variety E to one on UN? Examples
show this is not always possible. We will say that a pure N − 1 dimensional
subvariety E of UN is a special Rudin variety if there exists an annular domain
QN = {(z1,⋯,zN) ∈ CN : r < |zi| < 1,1 ≦ i ≦ N} for some r(0 < r < 1) and a δ > 0
such that
(i) E ∩ QN = ∅ and
(ii) if 1 ≦ k ≦ N and (z′,α,z′′) ∈ (Qk−1 × U × QN−k) ∩ E and
(z′,β,z′′) ∈ (Qk−1 ×U ×QN−k) ∩E and α≠β, then |α−β|≧ δ. Obviously (i) implies
that a special Rudin variety is a Rudin variety. We have the
Theorem. If E is a special Rudin variety in UN, then there exists a bounded
linear transformation T : H∞(E) → H∞(UN) (where H∞ is the corresponding
Banach space of bounded holomorphic functions under sup norm) which extends each
bounded holomorphic function on E to one on UN.
|