Translation kernels on discrete Abelian groups

Let G be a compact Abelian group with discrete countable dual group Γ = Ĝ and let f ∈ L¹(G) with Fourier transform F = f. If V is a finite subset of Γ we consider the operator F_V on L²(V ):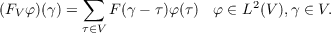

∑ (FVφ)(γ) = F(γ − τ)φ(τ) φ ∈ L2(V ),γ ∈ V. τ∈V

Then if {V _n} is any suitably restricted sequence of finite subsets of Γ we show that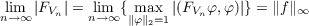

nli→m∞ |FVn| = nl→im∞{ max |(FVnφ,φ )|} = ∥f∥∞ ∥φ∥2=1

where |F_V| is the operator norm of F_V on L²(V ) and (F_Vφ,φ) denotes the inner product of F_Vφ and φ (over V ).

This result is then translated into a statement concerning a special class of infinite matrices which generalize the classical Toeplitz matrices. We then apply these results in evaluating the norm of a special type of linear operator.

Mathematical Subject Classification

Primary: 42.51

Secondary: 47.00

Milestones

Received: 14 April 1967

Revised: 22 November 1968

Published: 1 June 1969

Authors

William Richard Emerson

Vol. 29, No. 3, 1969

William Richard Emerson

Abstract

Mathematical Subject Classification

Milestones

Authors