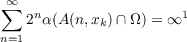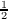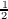|
Let K be a compact subset of
the complex plane and let Ω denote its complement. In 1966 Vituskin [11] proved the
following generalization of Mergelyan’s celebrated theorem on rational approximation
[9].
Theorem. (Vituskin). If each boundary point of K is a boundary point of some
component of Ω then A(K), the subset of continuous functions on K which are
analytic on the interior of K, is the same as R(K), the uniform closure of the rational
functions with poles in Ω.
The complexity of Vituskin’s techniques justifies the development of alternate
approaches to this problem. For a complete discussion of Vituskin’s techniques and
results see [14]. The alternate approach we have in mind exploits a recent result of
Garnett and Glicksberg [5]. Namely, R(K) = A(K) if they have the same
representing measures for each point φ ∈ K.
We are unable, at present, to prove Vituskin’s result. However, if Ωi denotes the
i-th component of Ω, if A(n,z) denotes the annulus {(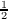 )n+1 ≦|ξ −z|≦ ( )n+1 ≦|ξ −z|≦ (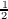 )n}, and if
α denotes analytic capacity, then we prove the following )n}, and if
α denotes analytic capacity, then we prove the following
Theorem. If K is such that (1) ∂(K), the boundary of K, has finitely many
components and (2) ∂K = {⋃
∂Ωi}∪{x1,x2,⋯}, where
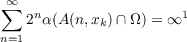
for each xk, then R(K) = A(K).
|