On the tensor products of von Neumann algebras

Jun Tomiyama

Vol. 30 (1969), No. 1, 263–270

DOI: 10.2140/pjm.1969.30.263

Abstract

Let A and B be C^∗-algebras and let A⊗_αB be their C^∗-tensor product with Turumaru’s α-norm. The author has previously defined mappings R_φ;A ⊗_αB → B and L_ψ : A ⊗_αB → A via bounded linear functionals φ on A and ψ on B, as follows: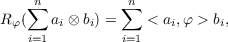

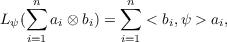and has shown how the families {R_φ|φ ∈ A^∗} and {L_ψ|ψ ∈ B^∗} determine the structure of the tensor product of A and B. Moreover, in a joint paper with J. Hakeda the author also proved the existence of these kinds of mappings in tensor products of von Neumann algebras and gave some of their applications. Further applications of these mappings are shown in the present paper.

Mathematical Subject Classification

Primary: 46.65

Milestones

Received: 8 January 1968

Published: 1 July 1969