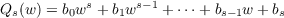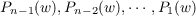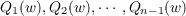|
An infinite set of algebraic
number fields is constructed; they are generated by a real algebraic irrational w,
which is the root of an equation f(w) = 0 with integer rational coefficients of degree
n ≧ 2. In such fields polynomials Ps(w) = a0ws + a1ws−1 + ⋯ + as−1w + as
and
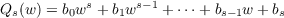
( s = 1,⋯,n − 1;ak,bk rational integers) are selected so that the Jacobi-Perron
algorithm of the n − 1 numbers
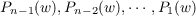
carried out in this decreasing order of the polynomials, and of the n − 1
numbers
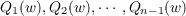
carried out in this increasing order of the polynomials both become periodic.
It is further shown that n − 1 different Modified Algorithms of Jacobi-Perron,
each carried out with n − 1 polynomials Pn−1(w),Pn−2(w),⋯,P1(w) yield
periodicity. From each of these algorithms a unit of the field K(w) is obtained by
means of a formula proved by the authors is a previous paper.
It is proved that the equation f(x) = 0 has n real roots when certain
restrictions are put on its coefficients and that, under further restrictions,
the polynomial f(x) is irreducible in the field of rational numbers. In the
field K(w)n − 1 different units are constructed in a most simple form as
polynomials in w; it is proved in the Appendix that they are independent; the
authors conjecture that these n − 1 independent units are basic units in
K(w).
|