|
|||||

|

|
|

|

|
|
Best constants in a
class of integral inequalities
David W. Boyd |
|
Vol. 30 (1969), No. 2, 367–383
|
Abstract |
|
In this paper a method is developed for determining best constants in inequalities of the following form: 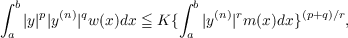 where y(a) = y′(a) = ⋯ = y(n−1)(a) = 0 and y(n−1) is absolutely continuous. It is first shown that for a certain class of m and w, equality can be attained in the inequality. Applying variational techniques reduces the determination of the best constant to a nonlinear eigenvalue problem for an integral operator. If m and w are sufficiently smooth this reduces further to a boundary value problem for a differential equation. The method is illustrated by determinin g the best constants in case (a,b) is a finite interval, m(x) ≡ w(x) ≡ 1, and n = 1. |
Mathematical Subject Classification
Primary: 26.70
|
Milestones
Received: 27 September 1968
Published: 1 August 1969
|
Authors |
| David W. Boyd | |
| Department of Mathematics University of British Columbia Vancouver BC V6T 1Z2 Canada |
|
| http://www.math.ubc.ca/~boyd/boyd.html | |
 |
