A subcollection of algebras in a collection of Banach spaces

Robert Paul Kopp

Vol. 30 (1969), No. 2, 433–435

DOI: 10.2140/pjm.1969.30.433

Abstract

Let D(p,r) with 1 ≦ p < ∞ and −∞ < r < +∞ denote the Banach space consisting of certain analytic functions f(z) defined in the unit disk. A function f(z) = ∑ _n=0^∞a_nzⁿ is a member of D(p,r) if and only if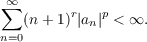

We define the norm of f in D(p,r) by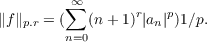

By the product of two functions f and g in D(p,r) we shall mean their product as functions, i.e., [f.g](z) = f(z)g(z). The purpose of this paper is to discover which of the spaces D(p,r) are algebras.

Mathematical Subject Classification

Primary: 46.55

Milestones

Received: 26 February 1968

Published: 1 August 1969