|
This paper is concerned with
the norm convergence of Banach space valued martingales in Orlicz spaces whose
underlying measure is (possibly) only finitely additive. Because of the possible
incompleteness of these Orlicz spaces of measurable point functions, this subject will
be treated in the setting of Orlicz spaces of set functions V Φ rather than the
corresponding spaces LΦ of measurable point functions. First, a conditionaI
expectation PB, operating on finitely additive set functions, is introduced and
related to the usual conditional expectation EB operating on L1 by the
equality
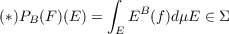
where (Ω,Σ,μ) is a measure space, B is a sub σ-field of Σ and F(E) = ∫
Efdμ for
E ∈ Σ.
Then, with the use of PB martingales of set functions are defined and their
convergence in appropriate V Φ spaces is investigated. In addition, in the countably
additive case, the results obtained for martingales of set functions are related to
martingales of measurable point functions and extensions of certain results of
Scalora, Chatterji, and Helms are obtained.
|