Note on some spectral inequalities of C. R. Putnam

Sterling K. Berberian

Vol. 30 (1969), No. 3, 573–575

DOI: 10.2140/pjm.1969.30.573

Abstract

It is shown that if A is any operator in Hilbert space and λ = re^i𝜃 is in the approximate point spectrum of A, then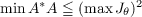

and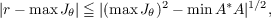

where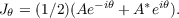

Several corollaries are deduced for arbitrary operators, generalizing results of C. R. Putnam on semi-normal operators.

Mathematical Subject Classification

Primary: 47.30

Milestones

Received: 26 November 1968

Published: 1 September 1969