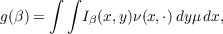|
A regular conditional measure ν
on a space Y relative to an outer measure μ on a space X is defined as a function on
X ×ℛ such that (1) for each x ∈ X,ν(x,⋅) is an outer measure on Y and ℛ is the
family of subsets of Y which are (Carathéodory) measurable under each of the
measures ν(x,⋅),x ∈ X, and (2) for each β ∈ℛ the function ν(⋅,β) on X is μ
integrable) i.e., ∫
ν(x,β)μdx ≦∞.
Letting g be the function on the subsets of Z = X × Y defined by
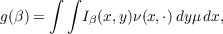
defining a covering family F to consist of those rectangles A × B where A is μ
measurable, B ∈ℛ and g(A×B) < ∞ or those sets N such that g(N) = 0, we obtain
the outer measure ϕ = (μ∘ν) on Z generated by (the content) g and covering family
F.
A system of regular conditional measures is a sequence begun by a measure ν0 on
a space X1 and followed by regular conditional measures νi (relative to μi) on spaces
Xi+1(i = 1,2,⋯) where μ1 = ν0 and μi+1 = (μi ∘νi) for i = 1,2,⋯ . Set X = ∏
xXi,
and for x ∈ X write xi for the point (x1,x2,⋯,xi) which is the projection of x onto
the space Xi = ∏
j=1iXj and similarly write Si = ∏
j=1iSj whenever the sets Sj are
subsets of Xj(j = 1,⋯,i).
For such a system of regular conditional measures a generalization of Tulcea’s
extension theorem for regular conditional probabilities holds, a Fubini-like
theorem for integrable functions is obtained and finally, for topological spaces, a
condition is given for the extension of inner regularity and almost Lindelöfness
properties.
|