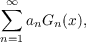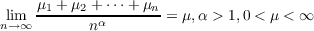|
Consider a sequence
{xn},n = 1,2,⋯ of random variables. Let Fn(x) be the distribution function of
Sn = ∑
k=1nxk and Hn(x), the distribution function of Mn = max1≦k≦nSk. Here
we study the asymptotic behaviour of
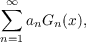 | (1.1) |
where Gn(x) is to mean either Fn(x) or Hn(x) (so that if a property holds for both
Fn(x) and Hn(x) it holds for Gn(x) and conversely) and {an} a suitable positive
term sequence, when {xn} form
(i) a sequence of dependent random variables such that the correlation
between xi and xj is ρ,i≠j,i,j = 1,2,⋯ , 0 < ρ < 1,E(xi) = μi,i = 1,2,⋯
and
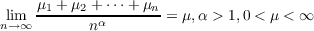 | (1.2) |
and
(ii) a sequence of identically distributed random variables with E(xi) = μ,i = 1,2,⋯
such that the correlation between xi and xj is ρij = ρ|i−j|,i,j = 1,2,⋯,0 < ρ < 1.
Suitable examples are worked out to illustrate the general theory.
|