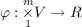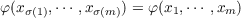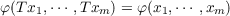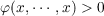|
Let V be an n-dimensional
vector space over the real numbers R and let φ be a multilinear functional,
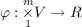 | (1) |
i.e., φ(x1,⋯,xm) is linear in each xj separately, j = 1,⋯,m. Let H be a subgroup of
the symmetric group Sm. Then φ is said to be symmetric with respect to H
if
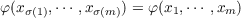 | (2) |
for all σ ∈ H and all xj ∈ V,j = 1,⋯,m. (In general, the range of φ may be a subset
of some vector space over R.) Let T : V → V be a linear transformation. Then T is
an automorphism with respect to φ if
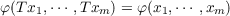 | (3) |
for all xi ∈ V,i = 1,⋯,m. It is easy to verify that the set A(H,T) of all φ which are
symmetric with respect to H and which satisfy (3) constitutes a subspace of the
space of all multilinear functionals symmetric with respect to H. We denote this
latter set by Mm(V,H,R).
We shall say that φ is positive definite if
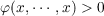 | (4) |
for all nonzero x in V , and we shall denote the set of all positive definite φ in
A(H,T) by P(H,T). It can be readily verified that P(H,T) is a convex cone in
U(H,T).
Our main results follow.
|