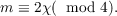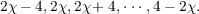|
Let M be a closed, connected,
nonorientable surface of Euler characteristic χ which is smoothly embedded in
Euclidean 4-space, R4, with normal bundle ν. The Euler class of ν, denoted by e(ν),
is an element of the cohomology group H2(M;𝒵) (the letter 𝒵 denotes twisted
integer coefficients). Since the group Hz(M;𝒵) is infinite cyclic, e(ν), is m times a
generator for some integer m. In a paper presented to a Topology Conference
held at the University of Michigan in 1940, H. Whitney studied the possible
values that this integer m could take on for different embeddings of the given
surface M. He gave examples to show that m can be nonzero (unlike the
case for an orientable manifold embedded in Euclidean space) and proved
that
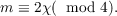
Finally, he conjectured that m could only take on the following values:
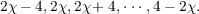
It is the purpose of the present paper to give a proof of this conjecture
of Whitney. The proof depends on a corollary of the Atiyah-Singer index
theorem.
|