|
|||||

|

|
|

|

|
|
Existence of a spectrum
for nonlinear transformations
John William Neuberger |
|
Vol. 31 (1969), No. 1, 157–159
|
Abstract |
|
Denote by S a complex (nondegenerate) Banach space. Suppose that T is a transformation from a subset of S to S. A complex number λ is said to be in the resolvent of T if (λI −T)−1 exists, has domain S and is Fréchet differentiable (i.e., if p is in ∕S there is a unique continuous linear transformation F = [(λI − T)−1]′(p) from S to S so that 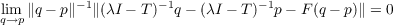 and locally Lipschitzean everywhere on S. A complex number is said to be in the spectrum of T if it is not in the resolvent of T. Suppose in addition that the domain of T contains an open subset of S on which T is Lipschitzean. Theorem. T has a (nonempty) spectrum. |
Mathematical Subject Classification
Primary: 47.80
|
Milestones
Published: 1 October 1969
|
Authors |
| John William Neuberger | |
 |
