On the sum ∑ ⟨nα⟩^−t and numerical integration

Seymour Haber and Charles Freeman Osgood

Vol. 31 (1969), No. 2, 383–394

DOI: 10.2140/pjm.1969.31.383

Abstract

Let “⟨x⟩” denote the distance of the real number x from the nearest integer. If α is an irrational number, the growth of the sum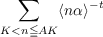

(A is a fixed number, > 1) as K →∞ depends on the nature of the rational approximations to α. We shall find estimates of this sum, for certain classes of irrational numbers. Part of the motivation for these estimates is an application to Korobov’s theory of numerical evaluation of multiple integrals.

Mathematical Subject Classification

Primary: 65.55

Milestones

Received: 12 December 1968

Published: 1 November 1969