Dilations of rapidly decreasing functions

Sav Roman Harasymiv

Vol. 31 (1969), No. 2, 395–402

DOI: 10.2140/pjm.1969.31.395

Abstract

Let S be the space of rapidly decreasing indefinitely differentiable functions on the n-dimensional Euclidean space Rⁿ, and suppose that ϕ ∈ S. We attempt to characterize the closed vector subspace of S which is generated by the set of all functions of the form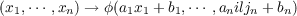

where a₁,⋯,a_n,b₁,⋯,b_n are real numbers, with a₁,⋯,a_n nonzero. We also consider an analogous approximation problem in the space S′ of temperate distribution on Rⁿ.

Mathematical Subject Classification

Primary: 46.40

Milestones

Received: 16 February 1968

Published: 1 November 1969