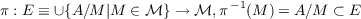|
Consider an f-algebra A
with identity (i.e., a,b,c ∈ A, αΛb = 0, c ≧ 0 ⇒ ca∧b = acΛb = 0) over the rationals
Q. Let ℳ be the maximal l-ideals of A.
THEOREM I. If 1 ≦ a ∈ A ⇒ 1∕a ∈ A, then each A∕M,M ∈ℳ is a totally
ordered division ring, and A can be embedded into a real f-algebra.
THEOREM II. A fiber-bundle or sheaf-like structure
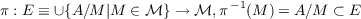
is constructed. Assume ∩ℳ = {0}; ℳ has the hull-kernel topology. All continuous cross
sections σ;ℳ→ E(π ∘σ = identity) form a partial algebra Γ(ℳ,E) containing an
isomorphic copy of A≅Â ⊆ Γ(ℳ,E). Let A∗ = {a ∈ A||a| < n1 some integer n}.
If
- 1 ≦ a ∈ A∗⇒ 1∕α ∈ A∗ then A≅ ⊆ Γ(ℳ,E), where  is order dense
in Γ(ℳ,E). If in addition
- A∗ is complete with respect to the absolute value |a|,a ∈ A,
then A≅Â = Γ(ℳ,E).
|