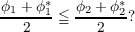|
The setting for the discussion is
a real linear space ℒ with an inner product (x,y). It is assumed that ℒ is complete
with respect to the norm generated by this inner product. Clearly the gauges on ℒ
and the bodies (closed, bounded, absolutely convex sets containing the origin 𝜃 as an
interior point) generate each other. The norm e(x) = (x,x) is a special
gauge; it is customary to write ∥x∥ instead of e(x). In general, a gauge will be
denoted ϕ(x), or briefly by ϕ; the symbol ϕ∗ represents the conjugate of
ϕ.
PROBLEM. Consider two gauges ϕ1 and ϕ2 such that e ≦ ϕ1 ≦ ϕ2. Under what
conditions may one conclude that
 | (*) |
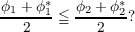That such an order relation may exist is suggested by the fact that for any gauge ϕ,
its “average” (ϕ + ϕ∗)∕2 is well behaving with respect to e, being always ≧ e.
Moreover, the average of the average is a better approximation to e, and so on.
Indeed, it is known that the sequence of successive averages converges decreasingly to
e.
SOLUTION. With each gauge ϕ (body K) we associate its spread S(x). The last
concept is a very natural one and is defined as follows: For 𝜃≠x ∈ℒ, consider the line
joining 𝜃 and x. Let ω(x) represent the (width) distance between the two support
hyperplanes of K orthogonal to that line, while δ(x) represents the (diameter) length
of the chord of K lying on that line. We then define Sϕ(x) = SK(x) = ω(x) − δ(x).
Clearly, S(x) = S(λx) for λ≠0. It turns out that for any pair of gauges ϕ1 and ϕ2
such that e ≦ ϕ1 ≦ ϕ2, the relation Sϕ1 ≦ Sϕ2 implies inequality (∗) and also
ϕ1ϕ1∗≦ ϕ2ϕ2∗.
|
