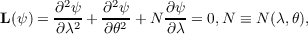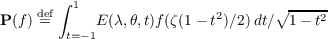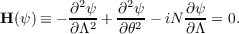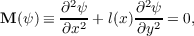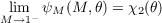|
In the case of the differential
equation
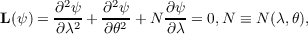
where N is an analytic function, the integral operator of the first kind
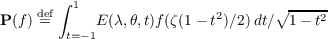
transforms analytic functions of a complex variable ζ = λ + i𝜃 into solutions of
L(ψ) = 0. Here E is a fixed function which depends only on L, while f(ζ) is an
arbitrary analytic function of the complex variable ζ;f is assumed to be
regular at ζ = 0. Using this operator, one shows that many theorems valid
for analytic functions of the complex variable can be generalized for the
solutions ψ of L(ψ) = 0. Continuing ψ(λ,𝜃) to complex values U = λ + iΛ and
setting λ = 0, one shows that many theorems in the theorems in the theory
of functions of a real variable can be generalized to the case of solutions
of
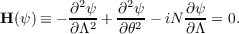
By change of the variables,
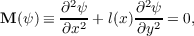
l(x) > 0 for x < 0,l(x) < 0 for x > 0,l(O) = 0, when considered for x < 0 can be
reduced to the equation L(ψ) = 0. The variables can be chosen so that U = 0
corresponds to x = 0. However, in this case the function N(λ) becomes singular at
λ = 0. Nevertheless, one can apply the theory of the so-called integral operators of
the second kind. If ψ(0,𝜃) = χ1(𝜃) and
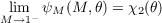
are given, one can determine the function f. Here M is the Mach number. In this
way one can determine from χ1 and χ2 the location and character of singularities of
ψ in the subsonic region. When considering ψ in the supersonic region, one can show
that some theorems on functions of one real variable can be generalized
to the case of certain sets of particular solutions ψν(Λ,𝜃),ν = 1,2,⋯ , of
H(ψ) = 0.
|