|
Let A be an n × n matrix
defined over a field F of characteristic greater than n. For each n × n matrix X we
define
![X1 = [A,X ]0 = X
Xh+1 = [A,X ]h = [A,Xh ] = AXh − XhA](a060x.png) | (1) |
for each positive integer h. Then X is defined to be k-commutative with A if and
only if
![[A,X ]k = 0, [A, X]k−1 ⁄= 0.](a061x.png) | (2) |
Let P(x) be a polynomial such that P(A)≠0. Specifically, assume that
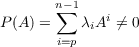 | (3) |
where p is a positive integer, each λi is a scalar from F, and λp≠0. In this paper we
study, for each positive integer k, the matrices X such that
![[A, X]k = P (A).](a063x.png) | (4) |
We specify a polynomial P(A) in the form (3) and show how the maximal value of
k for which (4) has a solution depends on the polynomial P(A). In Theorem 3 it is
assumed that A is nonderogatory. Since the only matrices which commute with A in
this case are polynomials in A, we are, in effect, establishing a more precise bound for
k in (2) by predetermining Xk.
In the derogatory case, a matrix which is not a polynomial in A may commute
with A. However, Theorem 4 shows that if we choose a polynomial P(A) as Xk, then
the maximal value of k depends on the polynomial P.
|





![X1 = [A,X ]0 = X
Xh+1 = [A,X ]h = [A,Xh ] = AXh − XhA](a060x.png)
![[A,X ]k = 0, [A, X]k−1 ⁄= 0.](a061x.png)
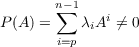
![[A, X]k = P (A).](a063x.png)
