A uniqueness theorem for second order quasilinear hyperbolic equations

Albert Emerson Hurd

Vol. 32 (1970), No. 2, 415–427

DOI: 10.2140/pjm.1970.32.415

Abstract

A uniqueness theorem is proved for weak solutions of quasilinear second-order hyperbolic equations of the form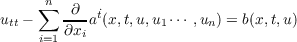

in many space variables. The weak solutions are assumed to satisfy a time-wise upper Lipschitz bound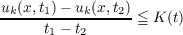

for all 0 < t ≦ t₁,t₂ where K(t) is an L¹-function. Together with the obvious assumptions, the equation is supposed to satisfy a symmetry condition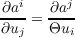

along with convexity of the aⁱ in u and u_k. As a corollary, a uniqueness theorem for systems proved by Oleinik is generalized.

Mathematical Subject Classification

Primary: 35.57

Milestones

Received: 13 September 1968

Revised: 30 June 1969

Published: 1 February 1970