Factorization of a special polynomial over a finite field

L. Carlitz

Vol. 32 (1970), No. 3, 603–614

DOI: 10.2140/pjm.1970.32.603

Abstract

Let q = p^z, where p is a prime and z ≧ 1, and put r = qⁿ, n ≧ 1. Consider the polynomial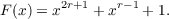

Mills and Zierler proved that, for q = 2, the degree of every irreducible factor of F(x) over GF(2) divides either 2n or 3n.

Mathematical Subject Classification

Primary: 12.25

Milestones

Received: 14 July 1969

Published: 1 March 1970