On the number of polynomials of an idempotent algebra. I

George Grätzer and J. Płonka

Vol. 32 (1970), No. 3, 697–709

DOI: 10.2140/pjm.1970.32.697

Abstract

This paper deals with the number p_n(A) of essentially n-ary polynomials of an idempotent universal algebra A. Under the condition that there is a commutative binary polynomial ⋅ it is proved that p_n+1(A) ≧ p_n(A) + (n− 1), provided p_n(A)≠1. If ⋅ is also associative this inequality is improved to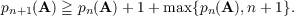

Mathematical Subject Classification

Primary: 08.30

Milestones

Received: 28 July 1969

Revised: 4 November 1969

Published: 1 March 1970