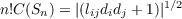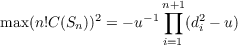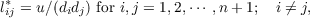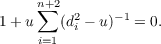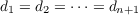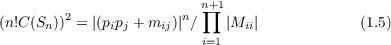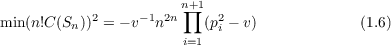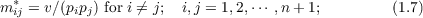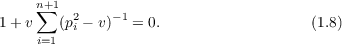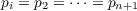On some extremal simplexes

Let A be a fixed point in n-dimensional Euclidean space. Let B₁,B₂,⋯,B_n+1 be the vertices of a simplex S_n of n-dimensions, that is, the n + 1 vertices do not lie on a (n − 1) dimensional subspace. Let d_i, assumed to be positive, be the distance of B_i from A, and let l_ij be the cosine of the angle between the straight lines AB_i and AB_j for i,j = 1,2,⋯ , n + 1. Let π_i denote the (n − 1)-dimensional hyperplane passing through all the vertices of S_n except B_i, let p_i, assumed positive, be the perpendicular distance of π_i from A, and let m_ij denote the cosine of the angle between the normals from A to π_i and π_j for i,j = 1,2,⋯,n + 1. The present paper deals with the following problems.

(a) An expression for the content of S_n,C(S_n) say, in terms of d_i and l_ij for i,j = 1,2,⋯,n + 1 is first obtained. Then leaving d₁,d₂,⋯,d_n+1 fixed, values of l_ij, say l_ij^∗, are determined in such a manner that C(S_n) is a maximum, and the maximum value of C(S_n) is obtained for the two cases that arise: (i) when A is inside S_n, (ii) when A is outside S_n. The latter case does not arise when d₁ = d₂ = ⋯ = d_n+1.

(b) An expression for C(S_n) is obtained in terms of p_i and m_ij,i,j = 1,2,⋯,n + 1. Then leaving p₁,p₂,⋯,p_n+1 fixed, values for m_ij, say m_ij^∗, are determined in such a manner that C(S_n) is a minimum, and such C(S_n) is computed for the two cases that arise depending on (i) whether A is inside S_n or (ii) A is outside S_n. The latter case does not arise when

p1 = p2 = ⋅⋅⋅ = pn+1.

The results are stated below.

(a) The content of S_n,maxC(S_n) and l_ij^∗ are given by

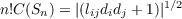n!C(Sn) = |(lijdidj +1)|1∕2

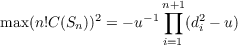(1.1)

2 −1n∏+1 2 max(n!C(Sn)) = − u (di − u) i=1

(1.2)

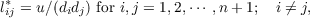∗ lij = u∕(didj) for i,j = 1,2,⋅⋅⋅ ,n + 1; i ⁄= j,

(1.3)

where u satisfies the equation

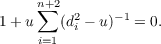n∑+2 2 −1 1 + u (di − u) = 0. i=1

(1.4)

The unique negative root for u in (1.4) corresponds to the case when A is inside S_n. When the relation

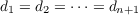
d1 = d2 = ⋅⋅⋅ = dn+1

is not satisfied, the smallest positive root for u in (1.4) corresponds to the case when A is outside S_n. Other roots for u in (1.4), if any, are inadmissible.

(b) The content iC(S_n), min(C(S_n)) and m_ij^∗ are given by

n∏+1 (n!C(Sn))2 = |(pipj + mij)|n∕ |Mii| (1.5) i=1

where |M_ii| is the cof actor of m_ii in |(m_ij)| and

2 −1 2nn∏+1 2 min(n!C (Sn )) = − v n (pi − v) (1.6) i=1

and

m∗ = v∕(p p) for i ⁄= j; i,j = 1,2,⋅⋅⋅ ,n+ 1; (1.7) ij ij

where v satisfies the equation

n∑+1 1+ v (p2i − v)−1 = 0. (1.8) i=1

The unique negative root for v in (1.8) corresponds to the case when A is inside S_n. When the relation

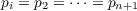
pi = p2 = ⋅⋅⋅ = pn+1

is not satisfied, the smallest positive root for v in (1.8) corresponds to the case when A is outside S_n. All other roots, if any, are inadmissible.

When d₁ = d₂ = ⋯ = d_n+1, we obtain the special result that the largest simplex inscribed in a sphere of n-dimensions is a regular one, while when p₁ = p₂ = ⋯ = p_n+1 the smallest simplex circumscribing a sphere is a regular one.

Mathematical Subject Classification

Primary: 52.40

Milestones

Received: 23 July 1969

Published: 1 April 1970

Authors

Mir Maswood Ali

Vol. 33, No. 1, 1970

Mir Maswood Ali

Abstract

Mathematical Subject Classification

Milestones

Authors