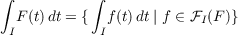|
Let I be a compact interval of
the real line and for each t in I, let F(t) denote a nonvoid subset of euclidean
n-space En. Let ℱI(F) be the collection of all Lebesgue summable functions
u;I → En having the property that u(t) ∈ F(t) almost everywhere on I.
Following the lead of Kudo and Richter, Aumann defines the integral of F over I
by
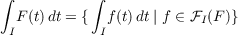
and, in addition to other results, establishes a dominated convergence theorem for
such integrals. Hermes has pursued Aumann’s line of thought to obtain results
concerning something akin to a “derivative” for set valued functions.
It is certainly also valid (and for control theoretic applications essential)
to define the trajectory integral of F to be the set 𝒮I(F) of all functions
which vanish at the left endpoint of I and have derivatives in ℱI(F). The
purpose of this paper is taken to be the study of the trajectory integrals of
nonvoid, compact set valued functions. A primary goal is the extension of the
results of Aumann to include the trajectory integral. A secondary goal is the
provision of an intuitively meaningful definition of “derivative” for set valued
functions.
|