|
This paper is a study of
boundedness and other properties of the solutions of nonlinear partial differential
equations of the form
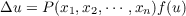 | (1.1) |
where P(x1,x2,⋯,xn) is positive, and u(x1,x2,⋯xn) is to be defined in some region
of Euclidean n-space, and Δu = ∑
i=1n∂2u∕∂xi2 is the Laplacian of u. In particular,
we consider the case f(u) = eu.
Our principal result is concerned with the nonexistence of entire solutions. An
entire solution u = u(x1,x2,⋯,xn) will be defined as a solution which though
continuous for 0 ≦ r < ∞ is twice continuously differentiable for 0 < 7⋅ < ∞.
Other results are concerned with the general form of and explicit bounds for
solutions.
|