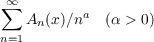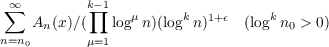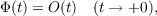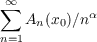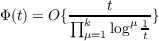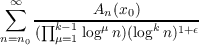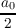On C, 1 summability factors of Fourier series at a given point

Fu Cheng Hsiang

Vol. 33 (1970), No. 1, 139–147

DOI: 10.2140/pjm.1970.33.139

Abstract

Let f(αj) be a function integrable in the sense of Lebesgue over the interval (−π,π) and periodic with period 2π. Let its Fourier series be

f(x)	∼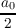 + ∑ n=1∞(a n cosnx + bn sinnx)
	≡∑ n=0∞A n(x).

Whittaker proved that the series

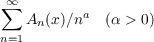
is summable |A| almost everywhere. Prasad improved this result by showing that the series

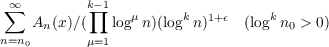
is summable |A| almost everywhere.

In this note, the author is interested particularly in the |C,1| summability factors of the Fourier series at a given point x₀.

Write

φ(t)

= f(x0 + t) + f(x0 − t) − 2f(x0),Φ(t)

= ∫ 0t|φ(u)|du.

The author establishes the following theorems.

Theorem 1. If

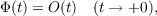
then the series

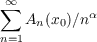
is summable |C,1| for every α > 0.

Theorem 2. If

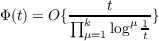
as t → +0, then the series

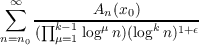
is summable |C,1| for every 𝜖 > 0.

Mathematical Subject Classification

Primary: 42.20

Milestones

Received: 28 February 1969

Published: 1 April 1970