Orthogonal groups of positive definite multilinear functionals

Stephen J. Pierce

Vol. 33 (1970), No. 1, 183–189

DOI: 10.2140/pjm.1970.33.183

Abstract

Let V be a finite dimensional vector space over the real numbers R and let T : V → V be a linear transformation. If φ : ×₁^mV → R is a real multilinear functional and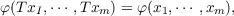

x₁,⋯,x_m ∈ V,T is called an isometry with respect to φ. We say φ is positive definite if φ(x,⋯,x) > 0 for all nonzero x ∈ V . In this paper we prove that if φ is positive definite and T is an isometry with respect to φ, then all eigenvalues of T have modulus one and all elementary divisors of T over the complex numbers are linear.

Mathematical Subject Classification

Primary: 15.80

Milestones

Received: 8 July 1960

Published: 1 April 1970