|
|||||

|

|
|

|

|
|
The principle of
subordination applied to functions of several variables
Ted Joe Suffridge |
|
Vol. 33 (1970), No. 1, 241–248
|
Abstract |
|
In this paper we consider univalent maps of domains in Cn(n ≧ 2). Let P be a polydisk in Cn. We find necessary and sufficient conditions that a function f : P−→ Cn be univalent and map the polydisk P onto a starlike or a convex domain. We also consider maps from 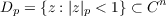 (1) ![n
∑ p 11p
|z|p = |(z1,z2,⋅⋅⋅ ,zn)|p = [ |zj|] ,p ≧ 1
j=1](a221x.png) into Cn and give necessary and sufficient conditions that such a map have starlike or convex image. |
Mathematical Subject Classification
Primary: 32.60
|
Milestones
Received: 19 May 1969
Published: 1 April 1970
|
Authors |
| Ted Joe Suffridge | |
 |
