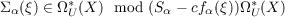|
This paper introduces into
cobordism theory a new notion borrowed from ordinary cohomology theory.
Specifically, let ξ be a U(n)-bundle over the CW-complex X. Let E and E0 be the
total spaces of the associated bundles whose fibers are respectively the unit disc
E2n ⊂ Cn and the unit sphere S2n−1 ⊂ Cn. The classifying map for ξ gives rise to an
element Uξ ∈ ΩU2n(E,E0). One defines the Thom isomorphism φ : ΩUq(X) →
ΩUq+2n(E,E0) by φ(x) = (p∗x)Uξ and Euler class, e(ξ) of ξ, by e(ξ) = p∗−1j∗(Uξ).
For each α = (α1,α2,⋯), let ofα(ξ) ∈ ΩU2|α|(X) be the Conner-Floyd Chern class
of ξ, and Sα : ΩUq(X,Y ) → ΩUq+2|α|(X,Y ) be the operation defined by
Novikov. Then one has the relation, Sα(e(ξ)) = cfα(ξ) ⋅ e(ξ). Now if ξ is a
bundle such that e(ξ) = 0, then one can define a secondary characteristic
class
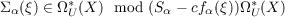
by using the above relation. The object of this paper is to study some of the
properties of such secondary characteristic classes.
|