Bergman kernel functions and the three types of canonical domains

Shozo Matsuura

Vol. 33 (1970), No. 2, 363–384

DOI: 10.2140/pjm.1970.33.363

Abstract

The objects of this paper are to extend J. Mitchell’s theorems on minimal domains of moment of inertia for sufficiently wider class ℱ and to discuss the relations among the three types of canonical domains in the ℱ-equivalent class. Some of the results are that, (i) a domain D is the minimal domain of moment of inertia of the [0,I_n;0]^D-equivalent class if and only if the following holds: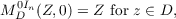

where M_D^0I_n(Z,0) is the minimizing function of the (0,I_n;0)_D-class, and (ii) if A,B and C are the sets of Bergman’s minimal domains, Bergman’s representative domains and Mitchell’s minimal domains of moment of inertia with the same center in the ℱ-equivalent class respectively, and if any one of the three relations A ∩ B≠ϕ, A ∩ C≠ϕ and B ∩ C≠ϕ holds, then it follows that A ⊃ B = C.

Mathematical Subject Classification

Primary: 32.25

Milestones

Received: 22 May 1969

Published: 1 May 1970