Ulm’s theorem for Abelian groups modulo bounded groups

Neal Hart

Vol. 33 (1970), No. 3, 635–640

DOI: 10.2140/pjm.1970.33.635

Abstract

Let  be the category of Abelian groups, B the class of bounded Abelian groups. It is shown that if G and H are totally projective p-groups, then G≅H in the quotient category Â∕B if and only if there exists an integer k ≧ 0 such that for all ordinals α and all integers r ≧ 0,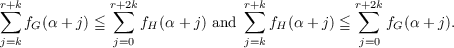

This extends a similar result of R. J. Ensey for direct sums of countable reduced p-groups. It is also noted that if G and H are totally projective p-groups, then G is quasi-isomorphic to H if and only if there exists an integer k ≧ 0 such that for all integers n ≧ 0 and r ≧ 0,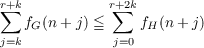

and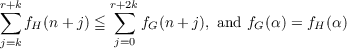

for all α ≧ ω. This extends a similar result of R. S. Pierce and R. A. Beaumont for direct sums of countable reduced p-groups.

Mathematical Subject Classification

Primary: 20.30

Milestones

Received: 4 December 1969

Published: 1 June 1970