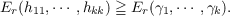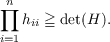An analysis of equality in certain matrix inequalities. I

William R. Gordon and Marvin David Marcus

Vol. 34 (1970), No. 2, 407–413

DOI: 10.2140/pjm.1970.34.407

Abstract

In this paper we are concerned with analyzing the cases of equality in certain inequalities that relate the eigenvalues and main diagonal elements of hermitian matrices.

Let E_r denote the r-th elementary symmetric function of k variables (E₀ = 1). If H = (h_τj) is an n-square positive semidefinite hermitian matrix with eigenvalues γ₁ ≦⋯ ≦ γ_n and if 1 ≦ r ≦ k ≦ n, then it is known that

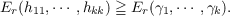(1.1)

If r > 1 and at least r of h₁₁,⋯,h_kk are positive then (1.1) can be equality if and only if there exists a permutation φ ∈_lS_k such that

(1.2)

where H_n−k is (n−k)-square and + denotes direct sum. Of course, if r = k = n then (1.1) is the Hadamard determinant theorem:

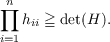(1.3)

If some h_ii = 0, then H is singular and (1.3) is equality. If h_ii > 0,i = 1,⋯,n, then the condition (1.2) yields the well-known criterion for equality in (1.3), namely H = diag(h₁₁,⋯,h_nn).

Mathematical Subject Classification

Primary: 15.55

Milestones

Received: 8 May 1969

Revised: 15 December 1969

Published: 1 August 1970