Operator-valued Feynman integrals of finite-dimensional functionals

Gerald William Johnson and David Lee Skoug

Vol. 34 (1970), No. 2, 415–425

DOI: 10.2140/pjm.1970.34.415

Abstract

Let C[a,b] denote the space of continuous functions x on [a,b]. Let {α₁,⋯,α_n} be an orthonormal set of functions of bounded variation on [a,b]. Let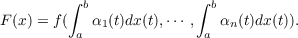

Recently, Cameron and Storvick defined certain operator-valued function space integrals, and, in particular, an operator-valued Feynman integral. In their setting, we give existence theorems as well as explicit formulas for the function space integrals of functionals F as above. We also study the properties of the operators which arise by “integrating” this type of functional.

Mathematical Subject Classification

Primary: 47.70

Secondary: 28.00

Milestones

Received: 22 August 1969

Published: 1 August 1970